Stunning-PS

트라이(Trie) 자료구조란? - Jiyeon

 
  • Jiyeon Lee
  • Apr 08, 2021

트라이 (Trie)

img

트라이(Trie)란 문자열을 저장하고 효율적으로 탐색하기 위한 트리 형태의 자료구조입니다. 보통 Prefix Tree, digital search tree, retrieval tree라고도 부릅니다. 트라이는 문자열을 key로 사용하는 동적인 set 또는 연관 배열을 저장하는 트리의 확장된 구조입니다.

트라이 자료구조는 문자열을 탐색하고자할 때 단순하게 하나씩 비교하면서 탐색을 하는 것보다 훨씬 효율적입니다. 단, 빠르게 탐색이 가능하다는 장점이 있지만 각 노드에서 자식들에 대한 포인터들을 배열로 모두 저장하고 있다는 점에서 저장 공간의 크기가 크다는 단점이 있습니다.

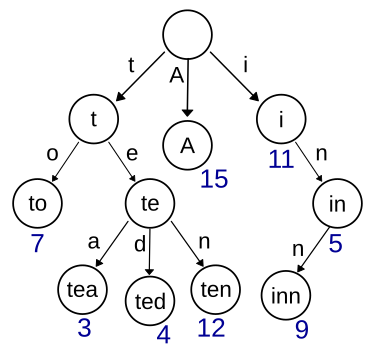
위 그림과 같이 트리의 루트에서부터 자식들을 따라가면서 생성된 문자열들이 트라이 자료구조에 저장되어있다고 볼 수 있습니다. 저장된 단어는 끝을 표시하는 변수를 추가해서 저장된 단어의 끝을 구분할 수 있습니다.

DFS형태로 검색을 해보면 사진의 번호에 나와있듯이 to, tea, ted, ten, A, i, in, inn이라는 단어들이 자료구조에 들어가있음을 알 수 있습니다.

구현 코드

1. 클래스로 구현

class TrieNode:
        # Initialize your data structure here.
        def __init__(self):
            self.word=False
            self.children={}
    
    class Trie:
    
        def __init__(self):
            self.root = TrieNode()
    
        # @param {string} word
        # @return {void}
        # Inserts a word into the trie.
        def insert(self, word):
            node=self.root
            for i in word:
                if i not in node.children:
                    node.children[i]=TrieNode()
                node=node.children[i]
            node.word=True
    
        # @param {string} word
        # @return {boolean}
        # Returns if the word is in the trie.
        def search(self, word):
            node=self.root
            for i in word:
                if i not in node.children:
                    return False
                node=node.children[i]
            return node.word
    
        # @param {string} prefix
        # @return {boolean}
        # Returns if there is any word in the trie
        # that starts with the given prefix.
        def startsWith(self, prefix):
            node=self.root
            for i in prefix:
                if i not in node.children:
                    return False
                node=node.children[i]
            return True
            
    
    # Your Trie object will be instantiated and called as such:
    # trie = Trie()
    # trie.insert("somestring")
    # trie.search("key")

시간 복잡도

문자열 집합의 개수와 상관 없이 찾고자하는 문자열의 길이가 시간 복잡도가 된다. 즉, 문자열의 길이가 $m$이라면 시간 복잡도는 $O(m)$

사실 빠른 시간안에 찾을 수 있는 장점이 있지만 가장 치명적인 단점은 공간복잡도입니다. 최종 메모리는 O(포인터 크기 * 포인터 배열 개수 * 트라이에 존재하는 총 노드의 개수) 가 되어 매우 커집니다.

예제 문제

백준 5052 전화번호 목록 : https://www.acmicpc.net/problem/5052

Search