- Binary Search 알고리즘이란?
- Binary Search 알고리즘 구현 방법
- 시간복잡도
- Binary Search 문제(leetcode 35)
- Binary Search 문제 모음
- 참고자료
Binary Search 알고리즘이란?
정렬된 배열의 탐색에 적합한 알고리즘으로, 정렬된 배열의 중앙에 있는 값을 조사하여 찾고자 하는 항목이 왼쪽 또는 오른쪽 부분 배열에 있는지 여부를 알아내어 탐색의 범위를 반으로 줄여가는 방법
예) 10억 명중에서 특정한 이름 검색
- Binary Search(이진 탐색): 단지 30번 비교 필요
- Sequence Search(순차 탐색): 평균 5억 번의 비교 필요
특징
- 모든 것을 방문하여 검색하는 Sequence Search 보다 효율적인 알고리즘
- 오름차순으로 정렬이 되어 있어야 하는 것이 조건 → 정렬된 리스트or배열
Binary Search 알고리즘 작동 방법
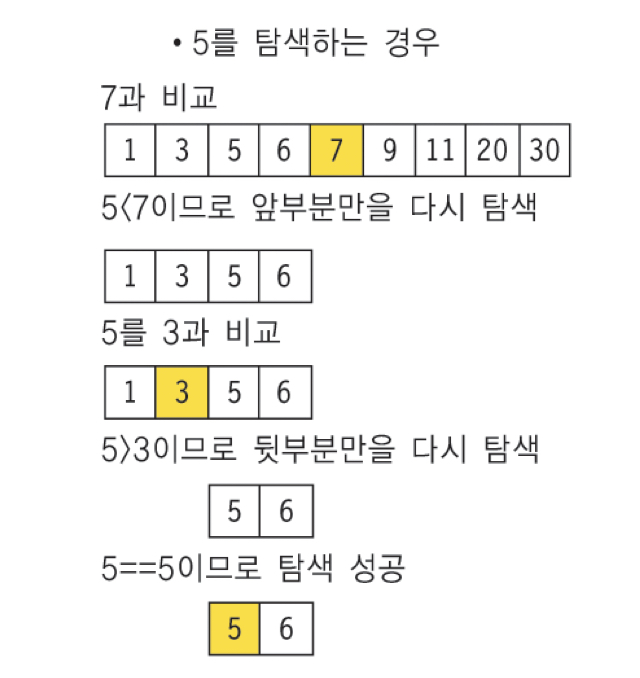
Binary Search 알고리즘 구현 방법
- 정렬된 배열의 양쪽 끝 값을 설정(left, right)
- 가운데를 항상 지정한 뒤 찾고자 하는 key와 mid를 비교하며
- key > mid → left = mid+1;
- key < mid → right = mid-1;
- key == mid → return mid
arr = 배열
key = 찾고자 하는 것
let right = arr.length-1;
let left = 0;
while(left <= right) {
let mid = Math.floor((right+left) / 2);
if(arr[mid] === key)
return mid;
else if(arr[mid] < key)
left = mid+1;
else
right = mid-1;
}
시간복잡도
Binary Search 알고리즘은 중간 값과 찾고자 하는 값을 비교하여 비교할때마다 탐색 범위가 1/2로 줄어든다.
자료의 갯수: N , 탐색 횟수: k
1/2^k*N = 1
N = 2^k
k = logN
결론적으로 시간복잡도는 logN 이다.
Binary Search 문제(leetcode 35)
https://leetcode.com/problems/search-insert-position/ -> 심플한 Binary Search 문제(Easy)
var searchInsert = function(nums, target) {
let left = 0;
let right = nums.length-1;
if(target === 0)
return 0;
while(left <= right) {
let mid = Math.floor((left+right) / 2);
if(nums[mid] === target)
return mid;
else if(nums[mid] < target)
left = mid+1;
else
right = mid-1;
}
return right+1;
};
Binary Search 문제 모음
참고자료
PREVIOUSTwo-Pointer 알고리즘 - Nathan