투포인터 (Two Pointers)
- 리스트에 순차적으로 접근해야 할 때 두 개의 점의 위치를 기록하면서 처리하는 알고리즘
- 정렬되어있는 두 리스트의 합집합에도 사용됨. 병합정렬(merge sort)의 counquer 영역의 기초가 되기도.
특정한 합을 가지는 부분 연속 수열 찾기
투포인터 알고리즘의 대표적인 부분.
- 시작점과 끝점이 첫번째 원소의 인덱스를 가리키도록 한다.
- 현재 부분 합이 M과 같다면 카운트한다.
- 현재 부분 합이 M보다 작다면 end를 1 증가시킨다.
- 현재 부분 합이 M보다 크거나 같다면 start를 1 증가시킨다.
- 모든 경우를 확인할 때까지 2-4번 과정을 반복한다.
그림과 함께 설명하기
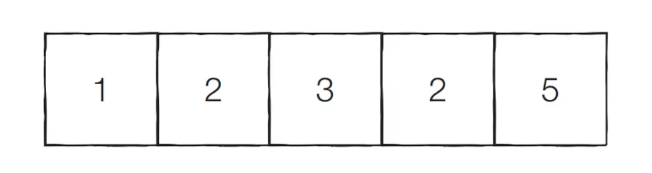
위와 같은 리스트와 $M=5$ 일 때의 예시를 생각해보자.
- [초기 단계] : 시작점과 끝점이 첫번째 원소의 인덱스를 가리키도록 한다.
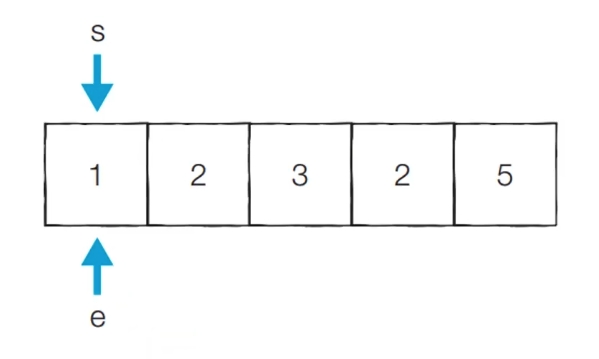
- 현재의 부분 합은 1.
- 현재 카운트 : 0
- [Step 1] : 이전 단계에서의 부분합이 1 -> end를 증가시킨다.
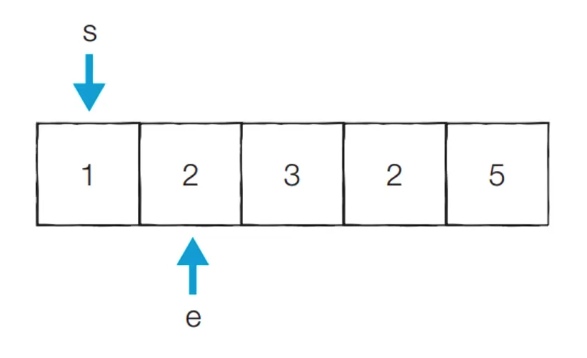
- 현재의 부분 합 : 3
- 현재 카운트 : 0
- [Step 2] : 부분합이 3 -> end를 증가시킨다
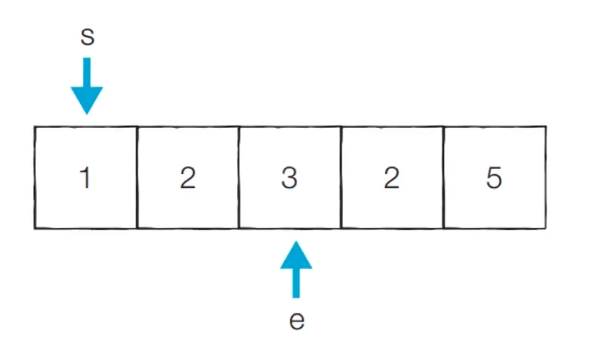
- 현재의 부분 합 : 6
- 현재 카운트 : 0
- [Step 3] : 부분합 6 -> start를 1 증가시킨다
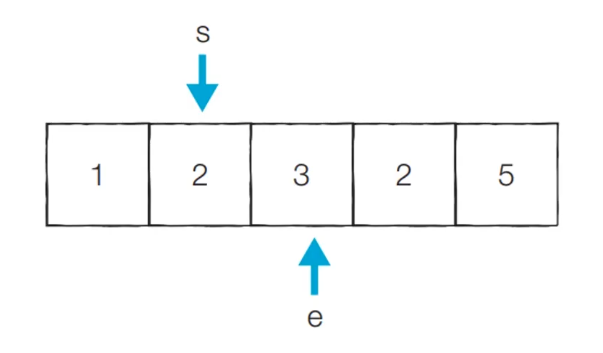
- 현재의 부분 합 : 5
- 현재 카운트 : 1 (부분합이 5이기 때문에)
- 이걸 계속 반복하다가 마지막
- [마지막]
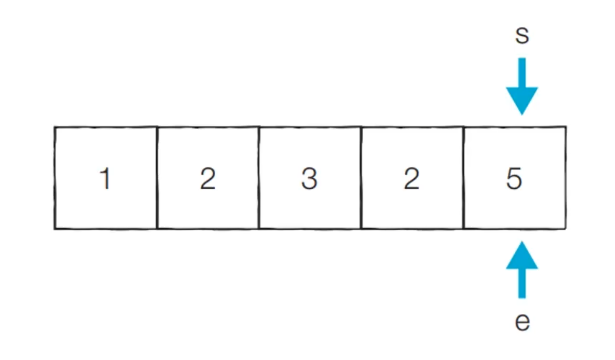
- 현재의 부분합 : 5
코드
n = 5 # 데이터의 개수 N
m = 5 # 찾고자하는 부분합 M
count = 0
interval_sum = 0
end = 0
# start를 차례대로 증가시키며 반복
for start in range(n):
# end만큼 이동시키기
while interval_sum < m and end < n:
interval_sum += data[end]
end += 1
# 부분합이 m일 때 카운트 증가
if interval_sum == m:
count += 1
interval_sum -= data[start]
print(count)
시간복잡도
\[O(N)\]매 루프마다 항상 두 포인터 중 하나는 1씩 증가하고 각 포인터가 n번 누적 증가해야 알고리즘이 끝난다 -> 각각 배열 끝에 다다르는데 $O(N)$ 이라 둘을 합해도 여전히 $O(N)$이다.
c.f> 슬라이딩 윈도우
투포인터처럼 구간을 훑으면서 지나간다는 공통점이 있으나 슬라이딩 윈도우는 어느 순간에도 구간의 넓이가 동일하다는 차이점이 있다.
Reference
PREVIOUSTwopointer Hankyul